I’ve often wondered what the simplest proof for the Pythagorean theorem is. By ‘simple’ I mean it contains the fewest steps, with the least amount of prerequisite knowledge.
I’ve always liked the James Garfield proof (I’ve even made a worksheet for students to complete based on it), but it does have a few bits of prerequisite knowledge: expanding double brackets, area of a trapezium, rearranging algebraic equations.
Here I present a proof that only depends on students understanding linear scale factors / similar shapes, and very basic algebra work.
Simple Proof
Start with a right triangle, sides a, b and c.
Now produce three similar triangles. Triangle 1 is created with a scale factor of a, triangle 2 with a scale factor of b, and triangle 3 with a scale factor of c.
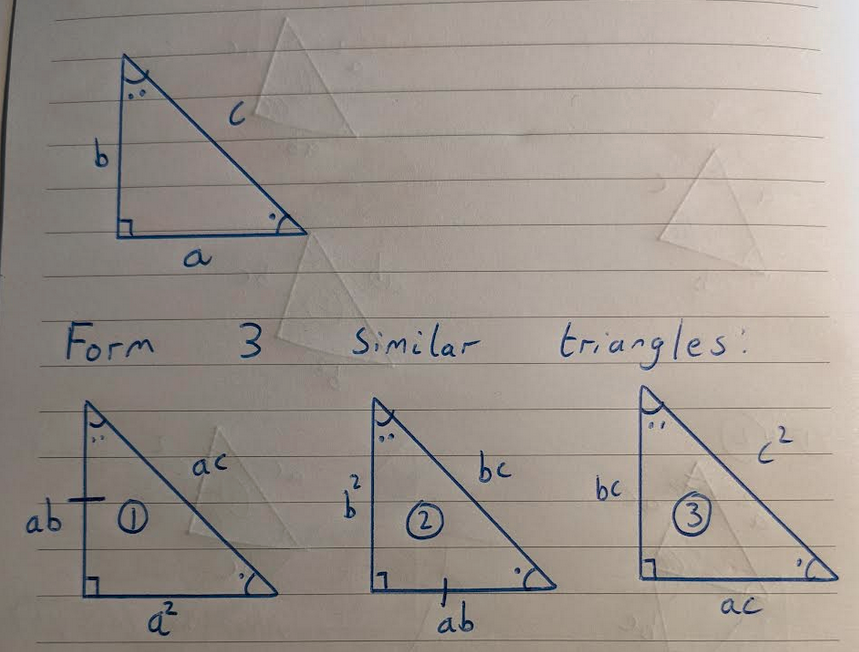
Notice that triangles 1 and 2 share a common side of ab. This means that these triangles can be placed together, to form triangle 4:
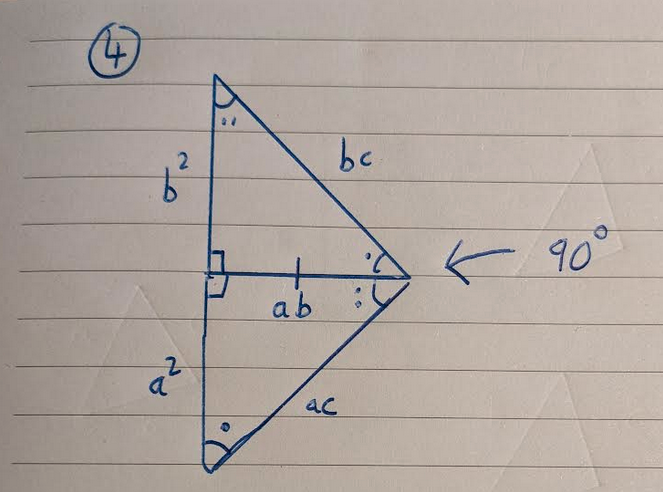
Notice now that triangle 3 and triangle 4 share the sides bc and ac. They also share two angles in common (and therefore three!) and hence are congruent. This implies a squared plus b squared is equal to c square.
End proof.
This proof is simply the well-known similar triangles proof (see e.g.). The similar triangles proof starts with triangle 4, draws the altitude (my line ab) and uses the ratios of the sides, and a bit of algebraic manipulation, to get the result. Maybe it’s just me, but I find hiding the ratios in the comfy notion of linear scale factors slightly simpler.
Maybe your students will too?
